martes, 31 de marzo de 2020
Ejemplos de cálculos del libro Probabilidad y Estadística para ingenieria y ciencias
viernes, 27 de marzo de 2020
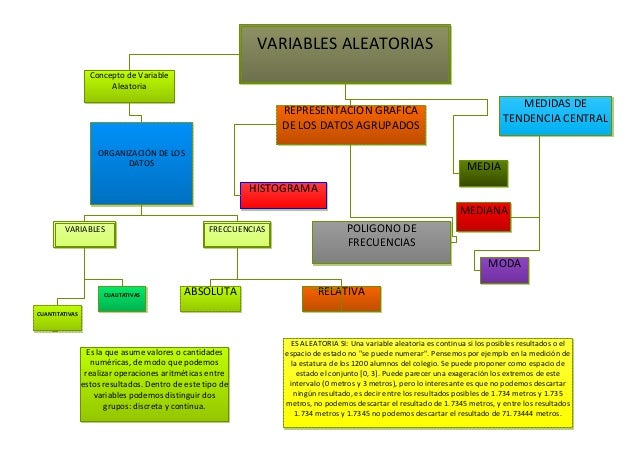
Distribucion normal
 La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
-caracteres morfológicos de individuos como la estatura;
-caracteres fisiológicos como el efecto de un fármaco;
-caracteres sociológicos como el consumo de cierto producto por un mismo grupo de -individuos;
-caracteres psicológicos como el cociente intelectual;
-nivel de ruido en telecomunicaciones;
 -errores cometidos al medir ciertas magnitudes;
-errores cometidos al medir ciertas magnitudes;-etc.
La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una "normalidad" más o menos justificada de la variable aleatoria bajo estudio.
En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.
Distribución binomial y distribución hipergeometrica y sus diferencias
Distribucion binomial
 En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, solo dos resultados son posibles. A uno de estos se denomina «éxito» y tiene una probabilidad de ocurrencia p y al otro, «fracaso», con una probabilidad2 q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, solo dos resultados son posibles. A uno de estos se denomina «éxito» y tiene una probabilidad de ocurrencia p y al otro, «fracaso», con una probabilidad2 q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
X-B(n,p)
La distribución binomial es la base del test binomial de significación estadística.
Distribución hipergeometrica
 La distribución hipergeométrica es una distribución discreta que modela el número de eventos en una muestra de tamaño fijo cuando usted conoce el número total de elementos en la población de la cual proviene la muestra. Cada elemento de la muestra tiene dos resultados posibles (es un evento o un no evento). Las muestras no tienen reemplazo, por lo que cada elemento de la muestra es diferente. Cuando se elige un elemento de la población, no se puede volver a elegir. Por lo tanto, la probabilidad de que un elemento sea seleccionado aumenta con cada ensayo, presuponiendo que aún no haya sido seleccionado.
La distribución hipergeométrica es una distribución discreta que modela el número de eventos en una muestra de tamaño fijo cuando usted conoce el número total de elementos en la población de la cual proviene la muestra. Cada elemento de la muestra tiene dos resultados posibles (es un evento o un no evento). Las muestras no tienen reemplazo, por lo que cada elemento de la muestra es diferente. Cuando se elige un elemento de la población, no se puede volver a elegir. Por lo tanto, la probabilidad de que un elemento sea seleccionado aumenta con cada ensayo, presuponiendo que aún no haya sido seleccionado.La diferencia entre las distribuciones hipergeométrica y binomial
Tanto la distribución hipergeométrica como la distribución binomial describen el número de veces que un evento ocurre en un número fijo de ensayos. Para la distribución binomial, la probabilidad es igual para cada ensayo. Para la distribución hipergeométrica, cada ensayo cambia la probabilidad de cada ensayo subsiguiente porque no hay reemplazo.Utilice la distribución binomial con poblaciones tan grandes que el resultado de una prueba prácticamente no tiene efecto sobre la probabilidad de que el próximo resultado sea un evento o un no evento. Por ejemplo, en una población de 100,000 personas, 53,000 tienen sangre O+. La probabilidad de que la primera persona seleccionada aleatoriamente en una muestra tenga sangre O+ es 0.530000. Si la primera persona en una muestra tiene sangre O+, entonces la probabilidad de que la segunda persona tenga sangre O+ es 0.529995. La diferencia entre estas probabilidades es lo suficientemente pequeña como para ignorarla en la mayoría de las aplicaciones.
Utilice la distribución hipergeométrica con poblaciones que sean tan pequeñas que el resultado de un ensayo tiene un gran efecto en la probabilidad de que el próximo resultado sea un evento o un no evento. Por ejemplo, en una población de 10 personas, 7 personas tienen sangre O+. La probabilidad de que la primera persona seleccionada aleatoriamente en una muestra tenga sangre O+ es 0.7000. Si la primera persona en la muestra tiene sangre O+, entonces la probabilidad de que la segunda persona tenga sangre O+ es 0.66667. La diferencia puede aumentar a medida que aumenta el tamaño de la muestra. La diferencia entre estas probabilidades es demasiado grande como para ignorarla en muchas aplicaciones.
Cuadro comparativo
|
DISTRIBUCION BINOMIAL |
DISTRIBUCIÓN HIPERGEOMÉTRICA |
|
·
En los experimentos que tienen este tipo de distribución, siempre
se esperan dos tipos de resultados, ejem. Defectuoso, no defectuoso, pasa, no
pasa, etc, etc., denominados arbitrariamente “éxito” (que es lo que se espera
que ocurra) o “fracaso” (lo contrario del éxito). ·
Las probabilidades asociadas a cada uno de estos resultados son
constantes, es decir no cambian. ·
Cada uno de los ensayos o repeticiones del experimento son
independientes entre sí. ·
El número de ensayos o repeticiones del experimento (n) es
constante. |
·
Al realizar un experimento con este tipo de distribución, se
esperan dos tipos de resultados. ·
Las probabilidades asociadas a cada uno de los resultados no son
constantes. ·
Cada ensayo o repetición del experimento no es independiente de
los demás. ·
El número de repeticiones del experimento (n) es constante. |
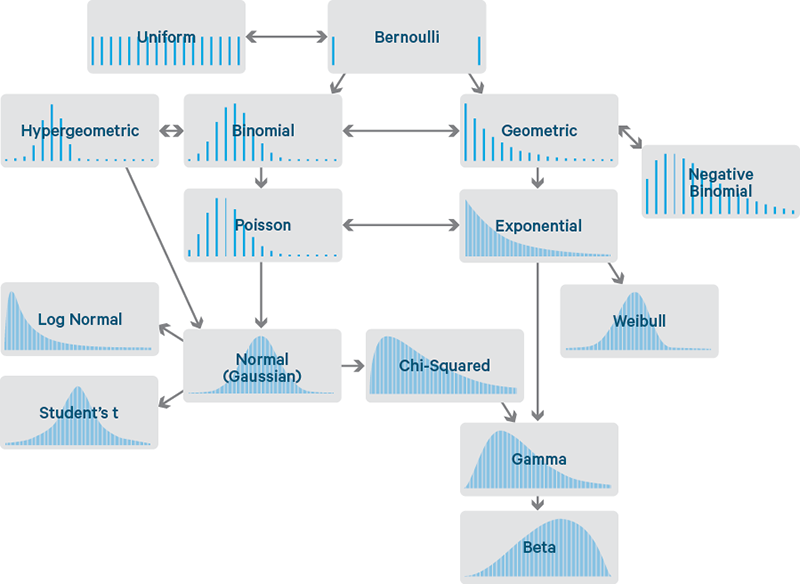
Distribuciones de probabilidad continuas y discretas y su representacion en la grafica
CONTINUAS

Discretas
Ejemplo del número de quejas de clientes
| x | P (X = x) |
|---|---|
| 5 | 0.037833 |
| 10 | 0.12511 |
| 15 | 0.034718 |
Esperanza Matematica
 La esperanza matemática, también llamada valor esperado, es igual al sumatorio de las probabilidades de que exista un suceso aleatorio, multiplicado por el valor del suceso aleatorio. O, dicho de otra forma, el valor medio de un conjunto de datos. Teniendo en cuenta, eso sí, que el término esperanza matemática está acuñado por la teoría de la probabilidad. Mientras que en matemáticas, se denomina media matemática al valor promedio de un suceso que ha ocurrido. En distribuciones discretas con la misma probabilidad en cada suceso la media aritmética es igual que la esperanza matemática.
La esperanza matemática, también llamada valor esperado, es igual al sumatorio de las probabilidades de que exista un suceso aleatorio, multiplicado por el valor del suceso aleatorio. O, dicho de otra forma, el valor medio de un conjunto de datos. Teniendo en cuenta, eso sí, que el término esperanza matemática está acuñado por la teoría de la probabilidad. Mientras que en matemáticas, se denomina media matemática al valor promedio de un suceso que ha ocurrido. En distribuciones discretas con la misma probabilidad en cada suceso la media aritmética es igual que la esperanza matemática.La esperanza matemática de una variable aleatoria X es el número que expresa el valor medio del fenómeno que representa dicha variable.
Calculo de la esperanza matemática